Bachelorarbeit Silas Birk Blume
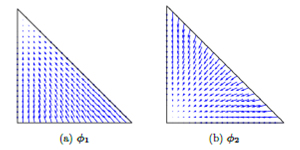
In der Arbeit wird zunächst die Membrangleichung hergeleitet und erläutert. Daraufhin werden die Bilinearformen für die drei Methoden bestimmt. Diese werden daraufhin unter Anwendung des Lemmas von Lax-Milgram sowie des Satzes von Brezzi bezüglich der Existenz einer eindeutigen Lösung untersucht, welche für alle rechten Seiten auffindbar ist. Es folgt die FE-Formulierung der verschiedenen Methoden unter Anwendung linearer Lagrange und Raviart-Thomas Elemente. Diese Formulierungen werden in Python implementiert. Die Implementierung der gemischten FEM wird hier abweichend vom Schema angegangen. Mit Hilfe der daraus entstehenden Programme folgt ein Vergleich des Konvergenzverhaltens für die einzelnen Methoden bezüglich der Verschiebungsvariable.
Zoom-Meeting beitreten:
https://tu-dortmund.zoom.us/j/94448258803?pwd=bmdrUWFwY010am5HYjIxZXJvMTFRUT09